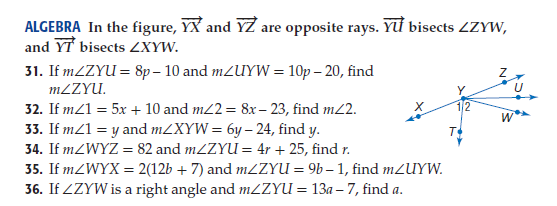Unit 1 Test

13. Unit 1 Review

13.  UNIT 1 REVIEW
-----------------------------------------------------------------------------------------------------------
LO:  I will review the concepts I learned about conjectures, angle relationships, logic and conditional statements.
-----------------------------------------------------------------------------------------------------------

Handout is as follows:

------------------------------------------------------------------------------------------------------------
DOL:
I will have completed at least two problems from each category.

11. Informal Proofs

For 9/12 Class:

11.  INFORMAL PROOFS
-----------------------------------------------------------------------------------------------------------
LO:  SWBAT will apply and use deductive reasoning, postulates and properties to prove mathematical statements.
-----------------------------------------------------------------------------------------------------------

We will mostly work on the handout which we will add to your notebook.

12. Formal Proof

For 9/13/13 class day:

11.  FORMAL PROOF
---------------------------------------------------------------------------------
LO:  SWBAT apply and use deductive reasoning, postulates and properties to prove geometrical statements using formal proofs
---------------------------------------------------------------------------------

Today is about proofs using geometric concepts.  We will be looking at several examples and then it's your turn. 

 Here are two examples:

Now it's your turn.  Try to fill in the blanks in these two proofs.
If  you do not finish in class, this becomes homework.

10. Algebraic Proofs

10.  ALGEBRAIC PROOFS

LO:  SWBAT will apply and use deductive reasoning to justify and prove mathematical statements

 Today is all about proving algebraic equations.

 

9. Laws of Syllogism and Detachment

9.  Law of Detachment and Syllogism

LO:  SWBAT use logical reasoning to prove statements are true and find counterexamples to disprove statements that are false

Venn Diagram

Can be used to represent a conditional statement

 

 

 

  

No Homework.

 

8. Conditional Statements

For September 9th class

8.  CONDITIONAL STATEMENTS
---------------------------------------------------------------------------------------------------------------------
LO:  SWBAT will determine the validity of a conditional statement, its converse, inverse
and contrapositive.
--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
(Textbook Chapter 2-3, starting from page 91)


1. Conditional Statements
To change a statement to an If-Then statement is to make a conditional statement.  

Let's look at the statement:  "Rain means it's cloudy."
Changing this to a conditional means identifying the hypothesis and conclusion then adding the if-then words to it like this:
 

The "if" is always followed by the hypothesis and the "then" is always followed by the conclusion.

Now you try.  Rewrite these advertisements into If-Then forms:

2.  Converse, Inverse, and Contrapositive
Other statements based on the conditional statements are Converse, Inverse and Contrapositive.  They are formed by exchanging and negating the hypothesis and conclusion of the conditional statements in various ways.

Notice that the symbols for the Conditional Statement reads as "p to q".

Now you try: using the same conditionals from the advertisements from section 1 above, write each one's converse, inverse and contrapositive.

3.  Counterexample
A Counterexample is a true example to prove a statement false.

For example:
Statement:  "If it has four right angles, then it's a square"
This is a false statement.  We then give the counterexample:  A rectangle.

The counterexample proves that the statement was false.

Now you try:  for each false statement from #2 above, provide a counterexample.

4.  Biconditional Statements

A conjunction of two statements where both the conditional and its converse are true is called biconditional. 

----------------------------------------------------------------------------------------------------------------------
Homework
Page 94, questions 1-10

7. Logical Reasoning

7. LOGICAL REASONING
--------------------------------------------------------------------------------------------------------
LO:  SWBAT use logical reasoning to prove statements are true and find counterexamples to disprove statements that are false.
 -----------------------------------------------------------------------------------------------------------------------------
Before we start, let's look at the format we will be using:

• Lower case letters will be used to name a statement.

 1. NEGATION

Negation is changing the truth value of a statement to its opposite value.  We designate the negated value with the symbol "~".

Example Statement:

p:  Austin is the capital city of Texas.    The truth value of this statement is True.  

~p:  Austin is NOT the capital city of Texas.  The truth value is now False.

Again, the ~p statement is the negated statement.

2. CONJUNCTION

A conjunction is a compound statement formed by joining two or more statements with the word and.  We then use the statements to write a compound statement.  (Compound just means mixing two things together in one). 

p:  Parallel lines have the same slopes

q:  Vertical angles are congruent

r:  The expression -5x + 11x simplifies to -6x

To write the compound statement, we use the symbol ∧.

So now we write our compound statements:

• p∧q (read as "p and q"):  Parallel lines have the same slope and vertical angles are congruent.
• ~p ∧ ~q (read as "not p and not q"):  Parallel lines DOES NOT have the same slope and vertical lines are NOT congruent.
• ~q ∧ r (read as "not q and r"):  Vertical angles are NOT congruent and the expression -5x + 11x simplifies to -6x.

3. DISJUNCTION

A disjunction is a compound statement formed by joining two or more statements with the word or.  We then use the statements to write a compound statement.

Let's use the same statements from above

p:  Parallel lines have the same slopes

q:  Vertical angles are congruent

r:  The expression -5x + 11x simplifies to -6x

To write the compound statement, we use the symbol  ˅ .

So now we write our compound statements:

So now we write our compound statements:

• p ˅ q (read as "p or q"):  Parallel lines have the same slope or vertical angles are congruent.
• ~p ˅ ~q (read as "not p or not q"):  Parallel lines DOES NOT have the same slope or vertical lines are NOT congruent.
• ~q ˅ r (read as "not q or r"):  Vertical angles are NOT congruent or the expression -5x + 11x simplifies to -6x.

Note that the statements are identical except they are now joined by the word "OR" instead of "AND".

4.  TRUTH TABLES

We will fill in this table in class and discuss it.

5.  VENN Diagrams

We will examine the Venn Diagram and interpret data from it.

-----------------------------------------------------------------------------------------------------------

Class Activity:

Handouts will be provided in class. 

----------------------------------------------------------------------------------------------------------

Homework:

P.87, questions 1 to 9.  The book is as below:

6. Homework

Here is the homework for those of you who need it.

6. Construction Explorations

6.  CONSTRUCTION EXPLORATIONS
--------------------------------------------------------------------------------------------------

LO:  SWBAT explore the attributes of segments, perpendiculars, angles and bisectors.
 -----------------------------------------------------------------------------------------------

These are the relationships we will use today to explore the attributes of our constructions.

Acute Angle

Right Angle

Obtuse Angle

Reflex Angle

Supplementary Angles

Complementary Angles

Linear Pairs

Midpoint

Congruent angles

Vertical angles

Adjacent angles

Perpendicular lines

Segment Addition Postulate

Angle Addition Postulate





Homework:
Page 36, questions 9 to 57, every 3rd question

5. Constructing angles and angle bisectors

Hello Class!  Please make sure you put down the following notes for class on 9/4/13.  Again, note that these go on the right side of your notebook.


5.  CONSTRUCTING ANGLES AND ANGLE BISECTORS
---------------------------------------------------------------------
LO:  SWBAT use constructions to explore the attributes of angles and angle bisectors.
----------------------------------------------------------------------

1. Constructing a copy of an angle
Please watch the following:  www.youtube.com/watch?v=cQ6v9muH2G8

Please write, in your own words, the steps to do this.


2.  Constructing an angle bisector
Please watch the following video:  www.youtube.com/watch?v=xFx6uHj16jE
Here is another version:  www.teachertube.com/viewVideo.php?video_id=228878

Write, in your own words, the steps to do this.


-------------------------------------------------------------------------------------

Class Activity:
Draw a triangle and construct each vertex's angle bisector.

4. Constructing Perpendiculars Through a Point

For Tuesday, 9/3/13, our topic is more on construction.

Lesson Objective (LO):  

SWBAT use constructions to explore attributes of perpendicular bisectors.

The two construction models we are doing are the following:  (Do these on the right side of your notebook)

1.  Constructing a perpendicular through a point on a line.

The first  half of this video:

http://www.teachertube.com/viewVideo.php?video_id=228903

Your job is to draw your own and write, in your own words, the steps needed to make this construction.

(Hint:  the first step is to draw a segment and put a point on it somewhere)

2.  Constructing a perpendicular through a point not on a line

This is the second half of the youtube video

Your job is to again draw your own and write, in your own words, the steps needed to make this construction.  (Hint:  the first step is to draw a segment and put a point somewhere above it.)

The final drawing for each of the above two tasks is going to look like this:

Class activity:  (Do this on the left side of your notebook)

1. Draw a triangle and on each side, construct its perpendicular bisector.  It's going to look like something like this:

Since the sides of your triangle won't be the same as above, your lines will be in different places.  But please note that each perpendicular bisector doesn't have to touch the opposite vertices.

2. Draw a triangle and on each side, construct a perpendicular line to the opposite vertex.  It's going to look something like below.  Yours, of course, can be different since your triangle will be different.  But please note that each line is perpendicular to the opposite point, which is the opposite vertex.